转载请注明出处:https://hts0000.github.io/
欢迎与我联系:hts_0000@sina.com
最小生成树
最小生成树问题,对应的图都是无向图。
最小生成树问题允许有负边
不能有环
Prim算法(普里姆算法)
Prim算法和Dijkstra算法很相似
朴素版Prim算法
稠密图用朴素版Prim算法,时间复杂度O(n^2)
算法步骤:
- 将所有点初始化为正无穷
- 迭代n次
- 每次找到不在集合当中的,距离集合最小的点t。集合表示已经加入生成树的点,距离集合最小定义为——点i到集合内任意一点的距离,是所有不在集合中的点中最小的。点i到集合的距离定义为——点i到集合内点的所有边中的最小值
- 用t更新其他点到集合的距离
- 把t加入集合
朴素版Prim算法代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
|
package main
import (
"fmt"
"bufio"
"os"
)
const N int = 510
const INF int = 0x3f3f3f3f
var (
in = bufio.NewReader(os.Stdin)
out = bufio.NewWriter(os.Stdout)
// 邻接矩阵存储图
g [N][N]int
// 点i到集合的距离
dist [N]int
// 点i是否在集合中
st [N]bool
n, m int
)
func prim() int {
// 初始化距离
for i := 1; i <= n; i++ { dist[i] = INF }
// res表示最小生成树各边权值和
res := 0
// 遍历n次
for i := 0; i < n; i++ {
t := -1
// 找到不在集合当中的,距离集合最近的点t
for j := 1; j <= n; j++ {
// j不在集合中
if ! st[j] && (t == -1 || dist[t] > dist[j]) {
t = j
}
}
// 把t点加入集合
st[t] = true
// 如果不是第一次找,而且不在集合中的点到集合最小距离是INF了,那么该图不是连通图
if i != 0 && dist[t] == INF { return INF }
// 累加权值和
if i != 0 { res += dist[t] }
// 用t更新其他点到集合的距离
for j := 1; j <= n; j++ {
dist[j] = min(dist[j], g[t][j])
}
}
return res
}
func main() {
defer out.Flush()
fmt.Fscan(in, &n, &m)
for i := 1; i <= n; i++ {
for j := 1; j <= n; j++ {
if i == j {
g[i][j] = 0
} else {
g[i][j] = 0x3f3f3f3f
}
}
}
for ; m > 0; m-- {
var a, b, c int
fmt.Fscan(in, &a, &b, &c)
// 无向图,建边的时候两个方向都建一次
g[a][b] = min(g[a][b], c)
g[b][a] = min(g[b][a], c)
}
// 如果不存在最小生成树,返回INF
// 存在则返回最小生成树各边的权值和
t := prim()
if t == INF {
fmt.Fprintln(out, "impossible")
} else {
fmt.Fprintln(out, t)
}
}
func min(a, b int) int {
if a < b { return a }
return b
}
|
经典模板题
858. Prim算法求最小生成树
堆优化版Prim算法
稀疏图用堆优化版Prim算法,时间复杂度O(mlogn),堆优化版Prim算法不如Kruskal算法简单好写,因此稀疏图一般使用Kruskal算法实现。
Kruskal(克鲁斯卡尔算法)
时间复杂度O(mlogm)
Kruskal算法是排序+并查集的应用,算法性能瓶颈主要在排序部分。
算法步骤:
- 对所有边排序O(mlogm)
- 枚举每条边a->b,权重c
- 如果a->b不连通,把这条边加入集合中,这一步用并查集来做O(m)
Kruskal算法代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
|
package main
import (
"fmt"
"bufio"
"os"
"sort"
)
const N int = 100010
const M int = 200010
// Kruskal算法只要能遍历到所有边即可
type Edge struct { a, b, w int }
var (
in = bufio.NewReader(os.Stdin)
out = bufio.NewWriter(os.Stdout)
// 并查集中的p数组,存储所有点
// 用于快速判断两个点是否在同一集合中
p [N]int
n, m int
)
// 寻找x的父节点,并做状态压缩,并查集的内容
func find(x int) int {
if x != p[x] { p[x] = find(p[x]) }
return p[x]
}
// 给定一个所有边的集合,返回是否存在最小生成树及最小生成树对应的权值和
func kruskal(edges []*Edge) (bool, int) {
var (
// 记录最小生成树对应的权值和
res int
// 记录已经联通的边数
// 连通n个点只需要n-1条边,用cnt来判断是否有最小生成树
cnt int
)
// 先对所有边根据边权从小到大排序
sort.Slice(edges, func(i, j int) bool { return edges[i].w < edges[j].w })
// 从小到大遍历所有边,得到的生成树就是最小的
for i := 0; i < m; i++ {
a := edges[i].a
b := edges[i].b
w := edges[i].w
// 用并查集判断a、b点是否在同一集合中
// 在同一集合中意味着,a、b点连通了
a, b = find(a), find(b)
// 如果a、b不连通
if a != b {
// 连通a、b
p[b] = a
// 累加边权和
res += w
// 记录生成树边数
cnt++
}
}
// 连接n个点,至少需要n-1条边,边数少于n - 1条,则图不存在最小生成树
return cnt < n - 1, res
}
func main() {
defer out.Flush()
fmt.Fscan(in, &n, &m)
for i := 1; i <= n; i++ { p[i] = i }
edges := make([]*Edge, 0, M)
for i := 0; i < m; i++ {
var a, b, w int
fmt.Fscan(in, &a, &b, &w)
edges = append(edges, &Edge{a, b, w})
}
flag, res := kruskal(edges)
if flag {
fmt.Fprintln(out, "impossible")
} else {
fmt.Fprintln(out, res)
}
}
|
经典模板题
859. Kruskal算法求最小生成树
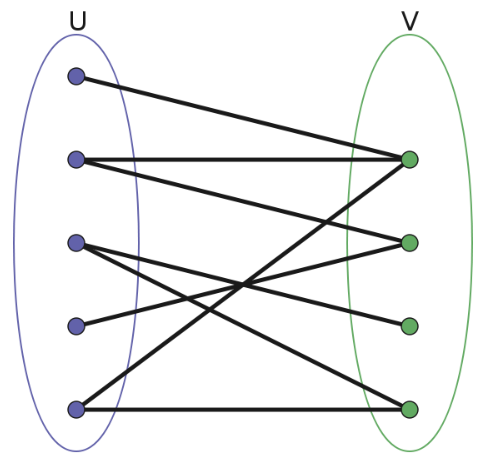
二分图
二分图指的是图中所有点能划分到两个集合中,所有的边都在两个集合之间连接,集合内部没有边。

二分图的题目通常是判断一个图是否是二分图。
一个图是二分图,当且仅当这个图不含有奇数环。反之,一个图不含有奇数环,那么它一定是一个二分图。
环是从一个点出发经过m条边后,能回到自身。奇数环指的是m为奇数。
当一个点i属于集合a时,那么所有与它连接的点j必须属于集合b。
由于图中不含奇数环,所以划分点到不同集合中的步骤一定不会矛盾。
染色法判断图是否为二分图
就是DFS,时间复杂度O(n + m)
染色过程就是把一个点确认颜色,比如白色,然后深度搜索把该点相连的其他点染为黑色。
染色法代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
package main
import (
"fmt"
"bufio"
"os"
)
const (
N int = 100010
M int = 200010
)
var (
in = bufio.NewReader(os.Stdin)
out = bufio.NewWriter(os.Stdout)
// 邻接表存储图
h [N]int
e, ne [M]int
idx int
// 存储改点染的什么颜色,1为白色,2为黑色
color [N]int
n, m int
)
func add(a, b int) {
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx++
}
func dfs(n, c int) bool {
// 先把当前点染为颜色c
color[n] = c
// 遍历该点所有邻边,将其他点染为另一种颜色
for i := h[n]; i != -1; i = ne[i] {
j := e[i]
if color[j] == 0 {
// 3 - c,当前颜色是1,其他点就染为2;当前颜色是2,其他点就染为1;
// 递归下去染色,任意一个连通块染色失败,就返回false
if ! dfs(j, 3 - c) { return false }
// 当前点与它连通的点颜色一样,发生矛盾
} else if color[j] == color[n] { return false }
}
return true
}
func main() {
defer out.Flush()
fmt.Fscan(in, &n, &m)
for i := 1; i <= n; i++ { h[i] = -1 }
for ; m > 0; m-- {
var a, b int
fmt.Fscan(in, &a, &b)
// 无向图
add(a, b); add(b, a)
}
flag := true
// 图不一定是连通图,所以需要遍历所有点,把每个连通块都尝试染色
// 如果有连通块染色失败,说明该图无法二分,也说明有奇数环
for i := 1; i <= n; i++ {
if color[i] == 0 {
if ! dfs(i, 1) {
flag = false
break
}
}
}
if flag {
fmt.Fprintln(out, "Yes")
} else {
fmt.Fprintln(out, "No")
}
}
|
经典模板题
860. 染色法判定二分图
匈牙利算法——二分图最大匹配问题
求二分图的最大匹配,时间复杂度最坏情况O(mn),实际运行情况远小于这个时间复杂度,效果很好。
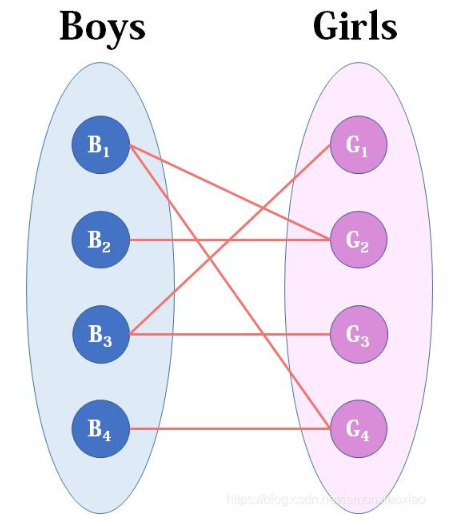
二分图最大匹配问题指的是,二分图中的集合a和集合b中的点,一一匹配的最大可能。
如图两个集合Boys和Girls,为每个男生匹配一个女生,最多能匹配多少个。

算法运行步骤:
- 遍历集合Boys
- 遍历Boys[i]的所有可匹配女生,任选一个匹配(如果是有权图,那么选权值最大的,就成为二分图的最优匹配)
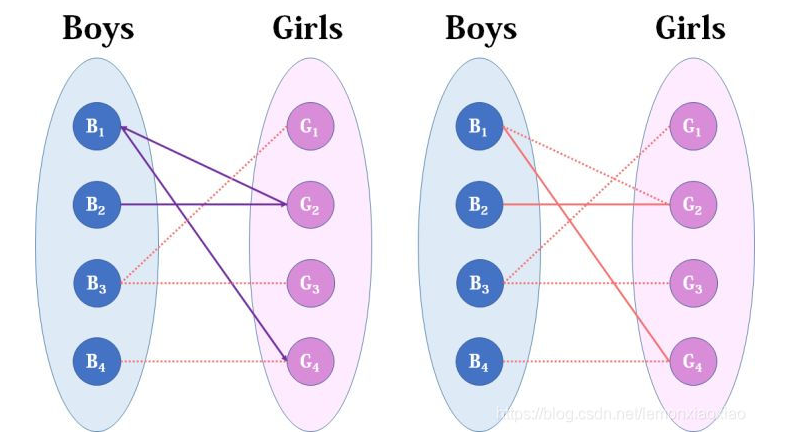
- 如果Boys[i]的所有可匹配女生都已经分配了
- 那么尝试让这些已匹配的人去匹配其他人,空出位置

图中B2只能匹配G2,但是G2已经被分配给B1了,那么尝试让B1匹配其他人,以增加匹配数。
算法运行完之后的情侣数量就是最大匹配数。
代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
|
package main
import (
"fmt"
"bufio"
"os"
)
const (
N int = 510
M int = 100010;
)
var (
in = bufio.NewReader(os.Stdin)
out = bufio.NewWriter(os.Stdout)
// 邻接表存储
h [N]int
e, ne [M]int
idx int
// 集合b的点匹配集合a的哪个点
match [N]int
// 集合a每个点遍历的时候,标记集合b那些点被访问了,避免递归时发生重复选择同一目标
// 递归子树去重
st [N]bool
// n1表示a集合有多少点,n2表示b集合有多少点,m表示边的数量
n1, n2, m int
)
func add(a, b int) {
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx++
}
// 寻找x能否匹配到一个集合b中的点
func find(x int) bool {
// 遍历集合a中点x能匹配的所有集合b中的点
for i := h[x]; i != -1; i = ne[i] {
// j是集合b中的点
j := e[i]
// 同一颗递归树中,j必须没被用过才能选
if ! st[j] {
// 这里把j标记为true,在下一层递归时,点j对应的点就不能再次匹配点j了,避免死循环
// 在同一颗递归树里面,点x不能再次匹配点j,必须找别的点,如果找不到,那么下面的判断就失败,不会赋值
// 回溯算法中的子树去重
st[j] = true
// j点没有匹配集合a中的点
// 或者点j对应的点,能匹配其他点
if match[j] == 0 || find(match[j]) {
// 实际记录时,记录的是集合b中哪个点与集合a中的点匹配
match[j] = x
return true
}
}
}
return false
}
func main() {
defer out.Flush()
fmt.Fscan(in, &n1, &n2, &m)
for i := 1; i <= n1; i++ { h[i] = -1 }
for ; m > 0; m-- {
var a, b int
fmt.Fscan(in, &a, &b)
// 虽然是无向图,但是算法遍历过程中只会从集合a找向集合b
// 所以b->a的边用不到
add(a, b)
}
// 匹配数量
res := 0
for i := 1; i <= n1; i++ {
// 每个点匹配开始都要把st清空,st只负责子树去重
// 是否匹配成功还要看match
for i := 1; i < N; i++ { st[i] = false }
// i能否匹配到一个点
if find(i) { res++ }
}
fmt.Fprintln(out, res)
}
|
经典模板题
861. 二分图的最大匹配