转载请注明出处:https://hts0000.github.io/
欢迎与我联系:hts_0000@sina.com
Trie树/字典树
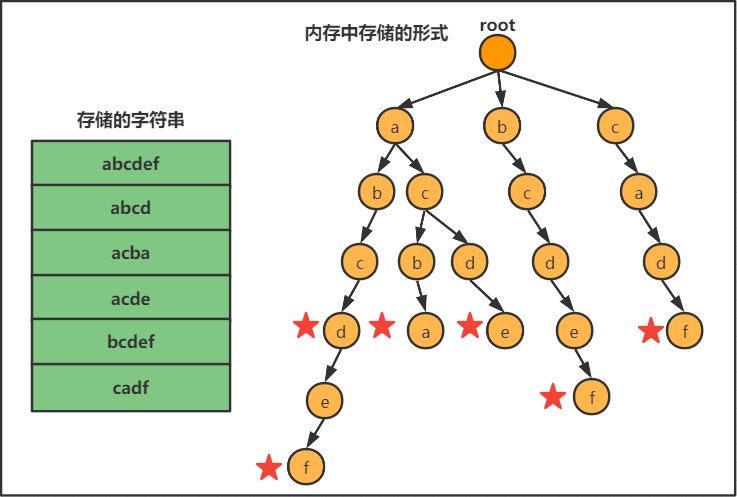
Trie是一种高效存储和查找字符串集合的数据结构。其存储形式如下图所示:

红色星号标记了存在以该词结尾的单词。
代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
package main
import (
"bufio"
"fmt"
"os"
)
const N int = 1e5 + 10
var (
// 指示son存储到哪了
idx int
// 第一个维度表示 节点i
// 第二个维度表示 节点i的子节点的下标
// 比如先存储了一个 只有a字母 长度为20的字符串,那么idx值为20
// 表示已经使用了20个节点
// 再存储新的字符串,将会从idx开始
// son[0][26]表示头结点的子节点
son [N][26]int
// 以某个节点结尾的单词数量
cnt [N]int
)
func insert(s string) {
p := 0
for i := 0; i < len(s); i++ {
u := s[i] - 'a'
if son[p][u] == 0 { // 如果没有存储过该字符,则新开一个节点存储,idx+1的含义
son[p][u] = idx + 1
idx++
}
p = son[p][u]
}
cnt[p]++ // 以节点p结尾的单词数量
}
func query(s string) int {
p := 0
for i := 0; i < len(s); i++ {
u := s[i] - 'a'
if son[p][u] == 0 { return 0 }
p = son[p][u]
}
return cnt[p]
}
func main() {
in := bufio.NewReader(os.Stdin)
out := bufio.NewWriter(os.Stdout)
defer out.Flush()
var n int
fmt.Scan(&n)
for ; n > 0; n-- {
var op, s string
fmt.Fscan(in, &op, &s)
if op == "I" {
insert(s)
} else {
fmt.Fprintln(out, query(s))
}
}
}
|
经典模板题
835. Trie字符串统计
208. 实现 Trie (前缀树)
143. 最大异或对
421. 数组中两个数的最大异或值
并查集
并查集通常用来:
- 将两个集合合并
- 询问两个元素是否在一个集合当中
并查集能在近乎O(1)的时间内完成这两个操作。
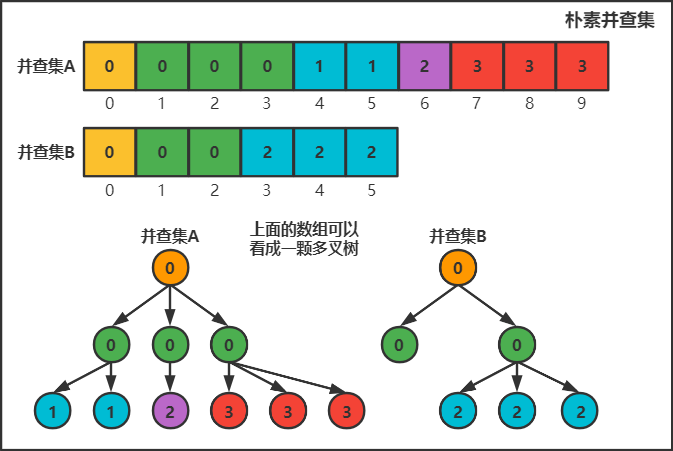
并查集是树形的数据结构,用数根来表示这个集合的编号,其余每个节点存储它的父节点是谁
朴素并查集

问题1:如何判断树根?
集合中只有树根的父节点等于自身,因此判断是否与父节点相同即可:if x == p[x]
问题2:如何求一个元素属于那个集合?
从num不断地向上走,一直走到树根:for x := x; x != p[x]; x = p[x] {}
问题3:如何合并两个集合?
假设有两个集合分别用编号x和y表示,则将集合x合并到y的操作为,将x的根节点指向y:p[x] = y
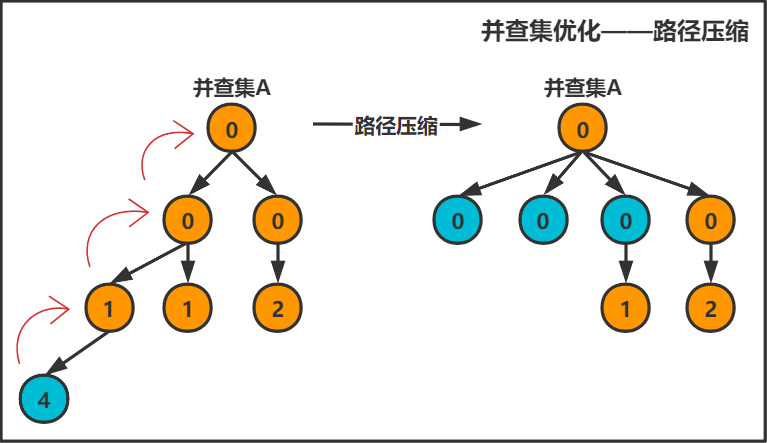
可以发现,并查集的时间复杂度集中在问题2上。并查集的路径压缩降低了这个时间复杂度。
有了路径压缩后,并查集查询两个元素是否在同一个集合中的时间复杂度,可以近乎看成O(1)。
在一次求元素属于那个集合的操作中,将查找路径上的所有节点直接指向根节点,本质上是降低了树的高度。
在代码实现时,一般会直接带上路径压缩。

代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
var p [N]int
func init() {
// 一开始每个元素都是一个单独的集合,自己就是自己的祖先节点
for i := 1; i <= n; i++ {
p[i] = i
}
}
// 核心实现,寻找 x 的祖先节点,并且加上路径压缩
func find(x int) int {
// 如果x的根节点不是,则递归寻找根节点,
// 并将这条路径上的节点的父节点都赋值为根节点
if p[x] != x { p[x] = find(p[x]) }
return p[x]
}
|
经典模板题
836. 合并集合
剑指 Offer II 118. 多余的边
维护每个集合数量
代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
// 额外使用一个cnt,来维护这个集合的数量
var p, cnt [N]int
func init() {
// 一开始每个元素都是一个单独的集合,自己就是自己的祖先节点
for i := 1; i <= n; i++ {
p[i] = i
// 初始化每个集合数量为1
cnt[i] = 1
}
}
// 核心实现,寻找 x 的祖先节点,并且加上路径压缩
func find(x int) int {
// 如果x的根节点不是,则递归寻找根节点,
// 并将这条路径上的节点的父节点都赋值为根节点
if p[x] != x { p[x] = find(p[x]) }
return p[x]
}
// 将b加入a集合,并且更新a集合数量
func merge(a, b int) {
a, b = find(a), find(b)
if a != b {
p[b] = a
cnt[a] += cnt[b]
}
}
|
经典模板题
837. 连通块中点的数量
记录偏移量
代码模板
1
2
3
4
5
6
7
8
9
10
11
|
const N int = 50010
var p, d [N]int
func find(x int) int {
if x != p[x] {
t := find(p[x])
d[x] += d[p[x]]
p[x] = t
}
return p[x]
}
|
经典模板题
240. 食物链
堆
堆是一颗完全二叉树,根据节点与其左右节点的性质,可以分为大根堆和小根堆。对于每一个节点,都小于其左右节点的堆称为小根堆,对于每一个节点,都大于其左右节点的堆称为大根堆。
堆通常需要支持如下操作:
- 插入一个数
- 求集合当中的最值
- 删除最值
- 删除任意一个元素(不常用)
- 修改任意一个元素(不常用)
要求执行完这些操作之后,集合仍然是一个堆。
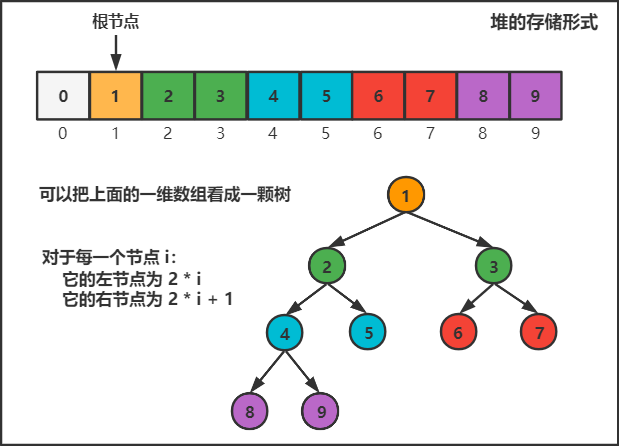
实现细节
我们使用一维数组来存储集合,将下标为1的位置定义为根节点,那么每个节点i与其左右节点的关系为:$左节点 = 2i,右节点 = 2i+1$。

我们定义两种操作:down(u int)和up(u int),分别从u向下调整堆,和从u向上调整堆。
down会判断u是否小于其左右节点(对于小根堆而言),如果不是,则交换u与最小者,再递归调整最小者。
up会判断u是否小于其父节点(对于小根堆而言),如果不是,则交换u与其父节点,再循环调整其父节点。
我们可以组合down和up操作,来实现上述需要支持的5个操作。
堆的初始化,我们可以不断的将数插到最后,然后向上调整堆,这样的时间复杂度是O(nlogn)的。有另一种方法是O(n)的。
对于一个数组,我们从n/2 ~ 1执行down操作,$n/2$其实就是倒数第二层,这一层的节点数量为$n/4$,只需要往下down一次,因此时间复杂度是$(n/4)*1$。往上每一层的节点数量为$n/8$,需要往下down两次,时间复杂度是$(n/8)*2$,以此类推,那么总的时间复杂度就是他们的总和:
$$sum((n/4)*1, (n/8)*2, (n/16)*3, …) = n$$
go语言中heap.Init函数也是采用这个实现。
代码模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// 堆
var h [N]int
// 堆存储长度
var size int
// 堆初始化 O(n)
func initHeap() {
for i := n / 2; i > 0; i-- { down(i) }
}
// 从u开始向上调整堆 O(logn)
func up(u int) {
for u / 2 > 0 && h[u] < h[u / 2] {
h[u], h[u / 2] = h[u / 2], h[u]
u /= 2
}
}
// 从u开始向下调整堆 O(logn)
func down(u int) {
t := u
// 拿到 u 及左右儿子中的最小值
if u * 2 <= size && h[u * 2] < h[t] { t = u * 2 }
if u * 2 + 1 <= size && h[u * 2 + 1] < h[t] { t = u * 2 + 1 }
// 如果 u 已经是 三者中最小,则不需要调整堆
// 否则交换 u 与最小者,递归调整堆
if u != t {
h[u], h[t] = h[t], h[u]
down(t)
}
}
|
经典模板题
838. 堆排序
839. 模拟堆
912. 排序数组