转载请注明出处:https://hts0000.github.io/
欢迎与我联系:hts_0000@sina.com
LRU(Least Recently Used)
计算机中内存是有限的,因此我们不可能将所有数据都存在内存中。根据程序的时空间局限性,我们总是希望内存中存储的是最新最近访问过的数据。因此我们需要一种页面置换算法,用来维护内存中始终是最新最近访问过的数据。
LRU就是一种常见的页面置换算法,其作用在于操作系统发生缺页中断时,将内存中最近最少使用的页面置换成需要读取内存的页面。
如何简单实现LRU算法
数据结构的设计
LRU缓存可以用哈希表+双向链表实现。
1
2
3
4
5
6
7
8
9
10
11
12
|
type LRUCache struct {
size int // cache已使用的大小
capacity int // cache容量大小
cache map[int]*Node
head, tail *Node
}
type Node struct {
val int
pre *Node
next *Node
}
|
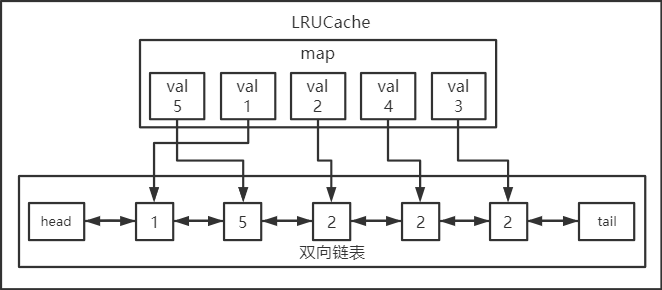
哈希表用来存储存储值到双向链表节点的映射,双向链表用来动态更新最近使用过的值。
大概示意如下图所示:

双向链表中越靠近头节点的,表示越近时间内访问过。设置head和tail节点标记边界,可以避免添加或删除节点时判断相邻节点是否存在,简化代码逻辑。
对于缓存,我们希望有如下操作,并且它们都在O(1)时间复杂度内完成:
- Get(key),根据输入的key找到对应的val
- Push(key, val),存储key/val的映射。如果cache已满,我们希望它自动淘汰最近最少使用的数据,再存储新数据。
Golang简单实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
|
type LRUCache struct {
size int
capacity int
// 值到双向链表节点的映射
cache map[int]*Node
// 双向链表
head, tail *Node // 虚拟头尾节点
}
type Node struct {
key, val int
pre *Node
next *Node
}
func NewNode(key, val int) *Node {
return &Node{
key: key,
val: val,
}
}
func Constructor(capacity int) LRUCache {
lru := LRUCache{
size: 0,
capacity: capacity,
cache: make(map[int]*Node, capacity),
head: NewNode(-1, -1),
tail: NewNode(-1, -1),
}
lru.head.next = lru.tail
lru.tail.pre = lru.head
return lru
}
func (this *LRUCache) Get(key int) int {
if _, ok := this.cache[key]; !ok {
return -1
}
node := this.cache[key]
// 更新该元素到链表头部,表示最近访问过
this.moveToHead(node)
return node.val
}
func (this *LRUCache) Put(key int, value int) {
// 如果缓存中没有该值,则将其添加到缓存中
if _, ok := this.cache[key]; !ok {
node := NewNode(key, value)
this.cache[key] = node
this.addToHead(node)
this.size++
// 如果超过缓存大小了,删除链表最尾元素,表示淘汰最近最近未使用的元素
if this.size > this.capacity {
removed := this.removeTail()
delete(this.cache, removed.key)
this.size--
}
} else { // 有该值则更新值和链表中的位置,
node := this.cache[key]
node.val = value
this.moveToHead(node)
}
}
// 以下操作都是O(1)时间复杂度
// 以下操作如果没有虚拟头尾节点,要增加很多判断
func (this *LRUCache) addToHead(node *Node) {
node.pre = this.head
node.next = this.head.next
this.head.next.pre = node
this.head.next = node
}
func (this *LRUCache) removeNode(node *Node) {
node.pre.next = node.next
node.next.pre = node.pre
}
func (this *LRUCache) moveToHead(node *Node) {
this.removeNode(node)
this.addToHead(node)
}
func (this *LRUCache) removeTail() *Node {
node := this.tail.pre
this.removeNode(node)
return node
}
|